1. Logikai elemek, relációk. De Morgan azonosságok. Logikai függvények szabályos (kanonikus) alakjai
- pneumatikus logikai elemek
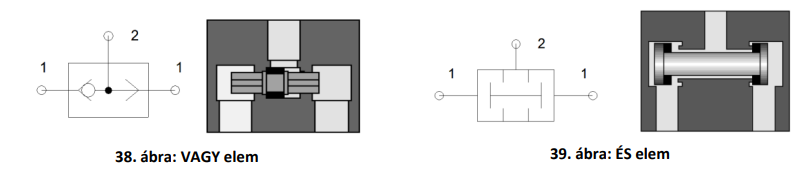
- De Morgan azonosságok:
$$ \overline{(a \land b)} = \overline{a}\lor\overline{b} $$ $$\overline{(a \lor b)} = \overline{a}\land\overline{b} $$
- De Morgan azonosságok általánosítva (Shannon szabálya):
$$\overline{[f(x_1, x_2,\ldots, x_n, \cdot, +)]} = f(\overline{x_1}, \overline{x_2}, \ldots, \overline{x_n}, +, \cdot) $$
- kanonikus forma
- a függvény olyan szisztematikus módon való megadása, melyben minden függvény csak egy módon adható meg
- (egyértelműség)
- mintermek
- logikai szorzatok összege
- Sum Of Products (SOP)
- diszjunktív forma
- pl. \(F(A,B,C)=m_1+m_3=\overline{A}\cdot\overline{B}\cdot C+\overline{A}\cdot B \cdot C\)
- minterm elnevezés → szűkítés (metszetképzés)
- logikai szorzatok összege
- maxtermek
- logikai összegek szorzata
- Product Of Sums (POS)
- konjunktív forma
- pl.: \(F(A,B,C) = M_1\cdot M_2 = (\overline{A}+\overline{B}+C)\cdot(\overline{A}+B+C)\)
- maxterm elnevezés → bővítés (unióképzés)
- logikai összegek szorzata